Justin Roche

Recently, I spent some time working on a new way to solve the “Interval Coloring” problem. If you’re unfamiliar with the problem itself, it goes as follows:

The Problem

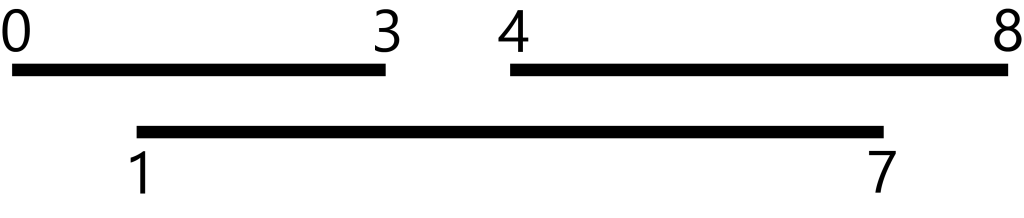
Given an array of intervals (like the ones shown above), report the maximum number of overlapping intervals. You can think of it like this: If these intervals are meetings, how many clones would you need in order to make it to every meeting? In the above example, the answer is 2.

Each interval has a start time and an end time. The typical interval coloring algorithm runs through the array of intervals in a queue and adds ‘colors’ to a ‘pool’ based on a set of conditions. This solution felt unintuitive to me, so I designed a different algorithm. Here’s the idea:

The Algorithm

• First, create two arrays, startTimes and endTimes, and load every interval’s start time and end time into the arrays.
• Merge-sort the arrays (or Radix-sort if possible). Notice that this breaks the link between each start time and its respective end time.
• Create integers startPointer, endPointer, overlaps, and maxOverlaps, and initialize each to 0.
• Run a loop, while startPointer is less than the length of the startTimes array. Within the loop, do the following:
  • If startTimes[startPointer] is less than endTimes[endPointer],
    • Increment overlaps and startPointer.
    • If overlaps is greater than maxOverlaps, set maxOverlaps to overlaps.
  • Else,
    • Decrement overlaps.
    • Increment endPointer.
• Report maxOverlaps.

Explanation & Analysis

The algorithm works by sweeping through the start and end times and changing the number of overlaps depending on whether an interval starts next or ends next. We can separate the start and end times because it doesn’t matter which interval is ending; it just matters that one of them is ending.

The complexity of the algorithm is O(n * log n). This is solely due to the merge-sort. This is not an improvement over alternative Interval Coloring algorithms, but practically speaking, the algorithm may have a slight advantage, because it doesn’t need to run through all start and end times, it only needs to run through all start times.

Thanks for reading!